Publikation in PNAS: Eine universelle Beschreibung für stochastische Oszillationen
Was haben der menschliche Herzschlag, das Blinken von Glühwürmchen und das Auf und Ab einer Kinderschaukel gemeinsam? Es sind alles Beispiele spontaner Oszillationen, das heißt rhythmisch auftretender Vorgänge. Oszillationen gibt es überall, und sie können auf den unterschiedlichsten physikalischen, chemischen oder biologischen Mechanismen beruhen.
Beteiligte Bernstein-Mitglieder: Benjamin Lindner
Die meisten Oszillationen sind „verrauscht”, das heißt mehr oder weniger irregulär. Der Herzschlag ist zum Beispiel nicht hundertprozentig regelmäßig; eine Herzratenvariabilität von 5 bis 10 Prozent wird gemeinhin als gesund angesehen. Solche stochastischen Oszillationen sind durch zufallsgeprägte Variationen in der Amplitude und im exakten zeitlichen Verlauf bestimmt. Sie sind mit sogenannten Bifurkationen dynamischer Systeme assoziiert und können auf ganz verschiedene Weise entstehen. Ihre theoretische Beschreibung schien daher bisher nur auf einer von Fall-zu-Fall-Basis möglich.
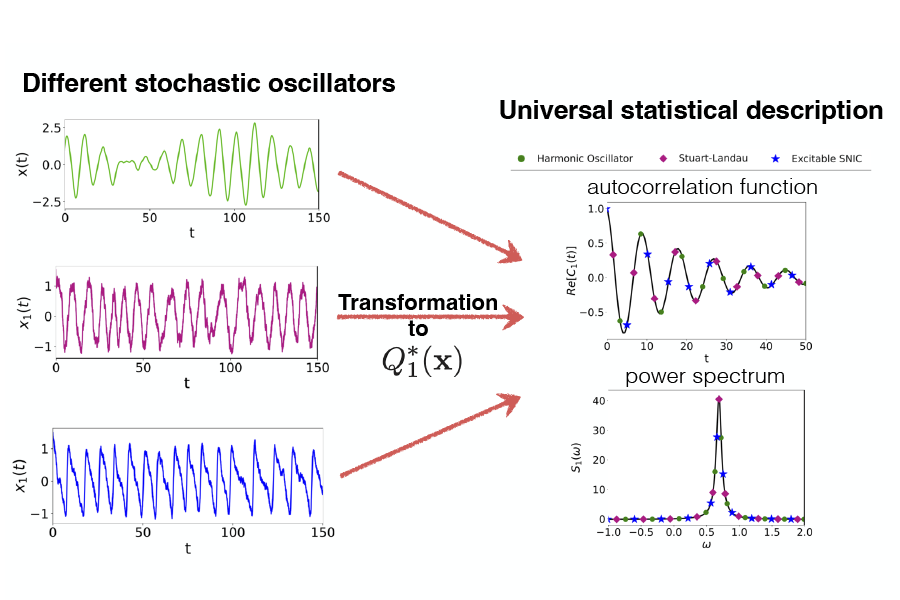
In einem Artikel, der gerade in der Fachzeitschrift PNAS erschienen ist, stellt ein interdisziplinäres Team aus der Physik, den Neurowissenschaften und der Mathematik ein neues Konzept einer universellen Beschreibung stochastischer Oszillatoren vor. Der Ansatz beruht auf der Verwendung komplexer Zahlen, um sowohl die zeitliche Phase als auch den Verlust der Oszillatorkohärenz über die Zeit zu beschreiben. Dieser neue Zugang macht es möglich, Oszillatoren zu vergleichen, die bisher als völlig unterschiedliche Systeme galten.
Der Mathematiker Peter Thomas von der Case Western Reserve University in Cleveland, Ohio, erläutert: „Moderne erdbebensicher gebaute Hochhäuser schwingen im Wind. Zufällige Windströme verschieben sie, aber ihre mechanischen Eigenschaften ziehen sie in ihre Ausgangslage zurück – wie eine Masse, die an einer Feder hängt. Man sollte nicht denken, dass diese Art der Bewegung viel mit einem Uhrpendel oder dem Stromfluss in einem elektrischen Schwingkreisgemein hat – aber unser neuer Formalismus gestattet, diese Phänomene zu vergleichen, Apfel-mit-Apfel, sozusagen.“
Im Zentrum der Arbeit steht eine mathematische Transformation auf eine neue Variable, die die Beschreibung in schlagender Weise vereinfacht. Der Physiker Benjamin Lindner von der Humboldt-Universität zu Berlin, in dessen Arbeitsgruppe die Kernidee ausgearbeitet wurde, erklärt dies so: „Verrauschte Oszillatoren kann man charakterisieren durch ihre zeitlichen Korrelationen, durch ihre Antwort auf externe Störungen und durch die Art, wie sie interagieren,wenn sie mit anderen Oszillatoren gekoppelt werden. Wenn wir uns die stochastischen Oszillatoren durch die Brille unserer neuen Variablen ansehen, folgen alle diese Charakteristiken sehr einfachen mathematischen Ausdrücken, die zudem alle exakt sind – es ist keine Näherung erforderlich.“
„Was diese Studie so spannend macht, ist der Umstand, dass Oszillationen allgegenwärtig sind, sobald man weiß, wonach man suchen muss“, sagt der theoretische Neurowissenschaftler Boris Gutkin von der Ecole Normal Superieure in Paris. „Für Satelliten, die die Erde umkreisen, für die Synchronisation von Leuchtkäfern in einem Baum, für Hirnrhythmen, die auftreten, wenn wir einem Gespräch folgen – für all diese Formen stochastischer Oszillationen haben wir eine wahrhaft universelle Beschreibung gefunden.“
Der Erstautor der Studie, Alberto Perez-Cervera, ein Mathematiker der Universidad Complutense de Madrid, sagt: „Die mathematische Transformation, die wir in der Arbeit vorschlagen, kann man als eine Art Brille auffassen, durch die sich verrauschte Oszillatoren betrachten lassen. Beim Blick durch diese Brille werden a priori sehr unterschiedliche komplexe Phänomene durch einfache, aber aussagekräftige universelle mathematische Formeln vergleichbar und kategorisierbar gemacht – wir denken, dass die Leser:innen unsere Begeisterung darüber teilen werden.“




